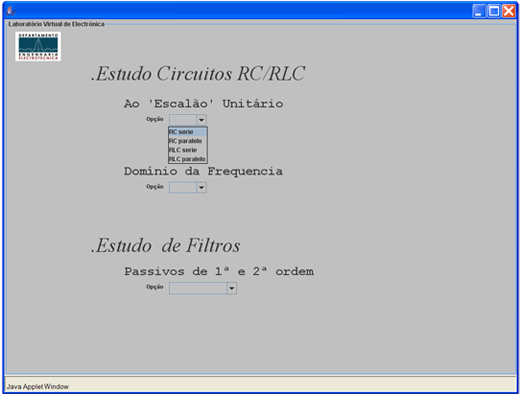
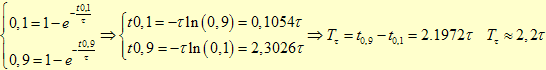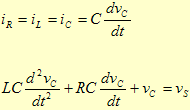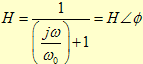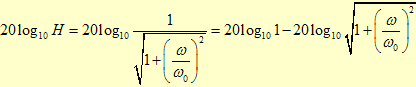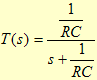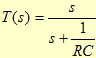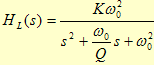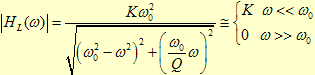Esta applet disponibiliza várias janelas ao utilizador, a primeira dá acesso à segunda janela, onde são disponibilizadas através de três menus o acesso aos diferentes circuitos que a applet permite simular. O utilizador deve introduzir correctamente o valor de todos os componentes do circuito e no final pressionar o botão "Resultados". Caso não sejam introduzidos todos os valores dos componentes dos circuitos, ou sejam introduzidos caracteres não desejados, o utilizador é informado com uma mensagem de erro.
- Introdução do valor de todos os componentes do circuito.
- Estudo de circuitos RC/RLC
- Ao Escalão unitário
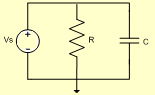
- Circuito RC série
- Circuito RC paralelo
- Circuito RLC série
- Circuito RLC paralelo
- Domínio da frequência
- Circuito RC série
- Circuito RC paralelo
- Circuito RLC série
- Circuito RLC paralelo
- Filtros passivos de 1ª e 2ª ordem
- Passa baixo de 1ª ordem
- Passa alto de 1ª ordem
- Passa baixo de 2ª ordem
- Passa alto de 2ª ordem
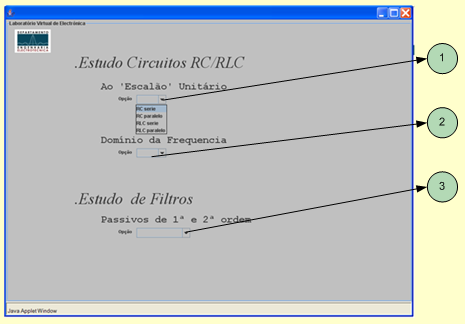
1 - Menu Opções relativas ao “escalão ” unitário: Dá a possibilidade de efectuar o estudo dos circuitos RC/RLC série e paralelo no tempo.
2 - Menu Opções relativas ao domínio da frequência: Dá a possibilidade de efectuar o estudo dos circuitos RC/RLC série e paralelo na frequência.
3 - Menu Opções relativas a filtros passivos de 1ª e 2ª ordem: Dá a possibilidade de efectuar o estudo dos filtros passa baixo e passa alto de 1ª e 2ª ordem.
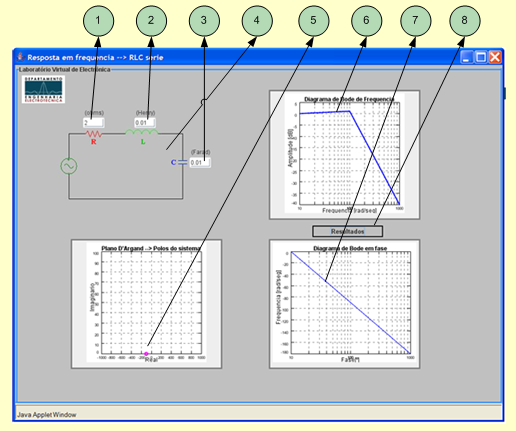
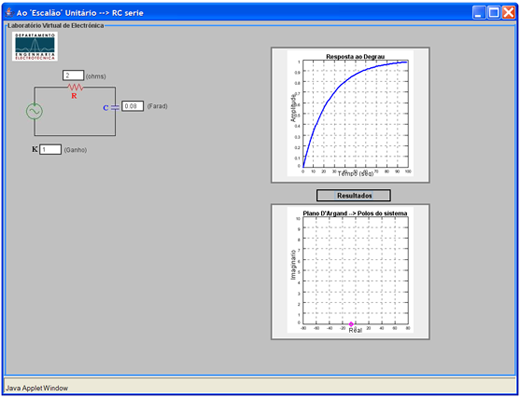
1 - Campo para introdução do valor da resistência em Ohm.
2 - Campo para introdução do valor da bobine em Henry.
3 - Campo para introdução do valor do condensador em Farad.
4 - Circuito que está a ser simulado.
5 - Gráfico que representa um plano de D'Argand onde são apresentados os polos do sistema.
6 - Gráfico que representa o diagrama bode de Frequência do circuito.
7 - Gráfico que representa o diagrama bode de Fase do circuito.
8 - Botão Resultados: Após premir são actualizados os campos 5, 6 e 7.
Degrau unitário é a função que anula para todos os valores do seu argumento que sejam menores que zero e que é um para todos os valores positivos do argumento.
Se x for o argumento e representarmos a função degrau unitário por U, então U (x) será zero para todos os valores de x menores que zero e, deste modo, será um para todos os x maiores que zero.
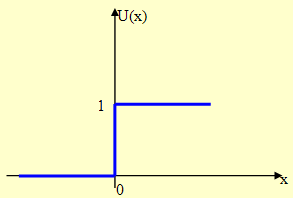
Em x=0, U(x) muda de 0 para 1. O valor para x=0 não é definido mas é conhecido para todos os valores arbitrariamente perto de x=0.
Este comportamento é indicado através de:
Definição matemática do Degrau Unitário:
Então:
sendo a sua transformada de Laplace:
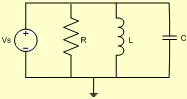
Circuito RC série:
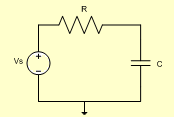
e sabendo que,
e
, temos
Resposta completa do circuito RC paralelo
Circuito RC paralelo:
Como estamos perante circuitos de primeira ordem, a saída, relaciona-se com a entrada,
através da equação
, em que k é o ganho do sistema e
a constante de tempo.
A função transferência será
em que
é o sinal de entrada e
é o sinal de saída.
Um sistema de primeira ordem possui uma equação característica com apenas uma singularidade, ou seja, um único pólo. O pólo do sistema está localizado sobre o eixo real no ponto de abcissa
.
A resposta ao degrau unitário será
em que
Pela transformada inversa temos
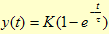
A constante de tempo do sistema (
seja igual a 0,632 do seu valor estacionário (quando t tende para infinito).
O tempo de subida
do sistema corresponde ao tempo necessário para que o sinal de saída
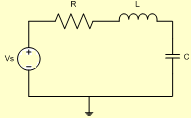
Circuito RLC série:
Sabendo que:
Resposta completa do circuito RLC paralelo
Circuito RLC paralelo:
Sabendo que:
Temos:
Nos circuitos de segunda ordem podemos ter vários tipos de sistema nomeadamente:
- Se
ambos os pólos da função transferência são reais negativos e iguais a
-> sistema sobre amortecido
Supondo que
a resposta ao degrau unitário será
- Se
os pólos são iguais reais e negativos e iguais a
-> sistema criticamente amortecido.
Supondo que
a resposta ao degrau unitário será
- Se
os pólos são complexos conjugados com partes reais negativas -> sistema sub amortecido.
Supondo que
a resposta ao degrau unitário será
- Se
os pólos estão no semi plano direito, logo o sistema é instável.
- Se os pólos se encontram no semi plano esquerdo, o sistema comporta-se como um sistema estável.
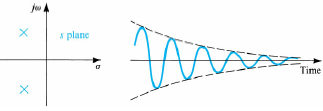
Para um sistema de segunda ordem cujo coeficiente de amortecimentoestá compreendido entre 0 e 1, temos os seguintes parâmetros:
- Tempo de pico
(só faz sentido calcular quando temos um sistema sub amortecido). É definido como o tempo necessário para que o sinal de saída alcance o ponto de amplitude máxima (máximo de sobre-elevação). Deste modo, é determinado pela expressão
- Sobre-elevação
é definida como a amplitude máxima que o sinal de saída atinge. (Só faz sentido calcular para sistemas sub amortecidos). Determina-se pela expressão
- Percentagem de sobre elevação (PO) é definida como a percentagem de sobre-elevação o quociente (em percentagem) entre o ponto de amplitude máxima e o valor final do sinal de saída. Determina-se pela expressão
- Tempo de estabelecimento
é definido como o intervalo de tempo necessário para que o sinal de saída alcance e se mantenha numa dada vizinhança do seu valor final. É expressa em termos percentuais pela letra
e é usualmente de 2% do valor final. Determina-se através de uma expressão aproximada, nomeadamente,
- Tempo de subida
é definido como o intervalo de tempo necessário para que o sinal de saída na sua subida inicial percorra o intervalo entre 10% e 90% do seu valor final. Se tivermos perante um sistema cujo factor de amortecimento seja de
Para um factor de amortecimento
. Para um factor de amortecimento
.
- O ganho estático é calculado pela seguinte expressão
e é calculado de igual forma para os três tipos de sistema.
A resposta em frequência de um sistema é a sua resposta em estado estacionário quando sujeito a uma entrada do tipo sinusoidal.
A saída do sistema é também um sinal sinusoidal, sendo que a relação entre a entrada e a saída, para cada valor de frequência, pode ser expressa em função de:
- Relação entre a amplitude do sinal de saída e a amplitude do sinal de entrada (resposta em amplitude);
- Diferença de fase entre o sinal de saída e o sinal de entrada (resposta em fase).
A resposta em frequência
associada a uma função de rede
obtém-se fazendo
.
Deste modo
e como a resposta em frequência é uma grandeza complexa, fica-se com
. O módulo é
e define-se por característica de amplitude, sendo o argumento igual a
definindo-se por característica de fase.
A resposta em frequência obtém-se a partir da relação entre as funções de rede e o regime forçado sinusoidal. Se a variável de entrada for sinusoidal
, a variável de saída também vai ser sinusoidal com a mesma frequência
, sendo a relação das amplitudes complexas a resposta em frequência,
.
Para se obter a característica de amplitude faz-se, o quociente das amplitudes das sinusóides
e a característica da fase obtém-se calculando a sua desfasagem
. A resposta em frequência obtém-se a partir dos pólos e dos zeros da função de rede correspondente. A partir
obtém-se
e
Através dos diagramas de Bode pode-se representar a resposta em frequência de um circuito. Estes consistem em dois traçados em função do logaritmo da frequência (especialmente espaçadas de décadas ou oitavas). O primeiro representa o módulo da função de transferência em dB (decibel). O segundo traçado representa o ângulo da função de transferência em ordenadas lineares.
Os diagramas de Bode apresentam algumas regras, nomeadamente:
- Para o diagrama de amplitude:
- À frequência de cada pólo o ganho é de -3dB;
- Após a frequência do pólo o declive é de -20dB por década (ou -6dB por oitava);
- À frequência de cada zero o ganho é de – dB;
- Após a frequência do zero o declive é de +20dB por década (ou +6dB por oitava).
- Para o diagrama de fase:
- À frequência de cada pólo o desfasamento é de -45º. Uma década antes é de 0º e uma década depois é de -90º, mantendo-se constante fora desse intervalo;
- À frequência de cada zero o desfasamento é de +45º. Uma década antes é de 0º e uma década depois é de +90º, mantendo-se constante fora desse intervalo.
Existem excepções, quando temos:
- Pólos na origem
- Se o sistema possuir n pólos na origem, o ganho à partida é de:
- E o desfasamento de:
- Zeros na origem
- Se o sistema possuir n zeros na origem, o ganho à partida é de:
- E o desfasamento de:
Obtém-se os diagramas de Bode usando as expressões
Em que
e
.
Ganho em dB será
Para baixas frequências
temos
e o ganho aproximado será
.
Para altas-frequências,
, temos
e o ganho aproximado será
.
A margem de ganho define-se como o inverso do valor que o diagrama do módulo possui quando o correspondente da fase passa por -180º. Dada pela expressão
A margem de fase define-se como 180º mais o valor que o diagrama de fase possui quando o correspondente do módulo passa por 0 dB. Dada pela expressão
Para o estudo de filtros recorre-se à utilização de circuitos lineares representados por uma rede de dois portos.
A função de transferência de um filtro será
Se o grau de numerador for menor que o grau do denominador, zeros em
. Para ser um sistema estável os pólos estão situados no semi plano esquerdo ou no eixo
(pólos simples).
A resposta em frequência será
, o ganho tem como expressão
, a atenuação é igual a
e o atraso é representado por
.
Em geral, a função transferência é determinada porem que
.
O numerador determina que tipo de filtro estamos perante.
Filtro passa-baixo:
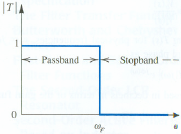
Estrutura geral:
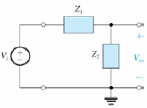
iremos ter
e
Circuito de um filtro passa baixo de 1ª ordem:
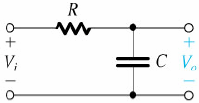
A função de transferência correspondente será:
Filtro passa alto:
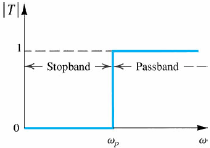
Circuito de um filtro passa alto de 1ª ordem:
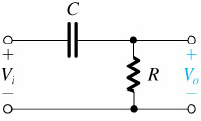
A função de transferência correspondente será:
A resposta em frequência dos filtros de segunda ordem é caracterizado por três parâmetros, nomeadamente, ganho K, frequência de corte
e factor de qualidade
.
Os filtros são projectados de modo a obter os valores requeridos para K,
A função de transferência é:
Quando o circuito em questão é estável, ou seja,
e
, substituindo s por
a função obtida será:
em que o ganho é dado por:
Circuito de um filtro passa baixo 2ª ordem:
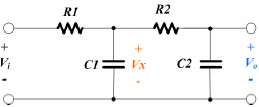
A função transferência do circuito será:
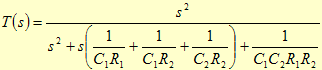
Filtro Passa Alto de segunda ordem
Circuito de um filtro passa alto 2ª ordem:
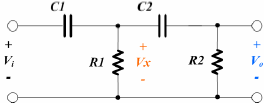
A função de transferência do circuito será:
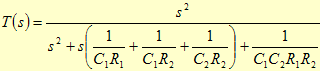
Uma entrada típica deste software consiste em defenir o valor da resistência, do condensador e o ganho do circuito. Ilustra-se o estudo do circuito RC série em resposta ao escalão unitário:
- Silva, Manuel de Medeiros, Introdução aos Circuitos Eléctricos e Electrónicos, Fundação Calouste Gulbenkian
- http://paginas.fe.up.pt/~amendon/TC-acetatos/acetatos-RLC.pdf
- Sedra / Smith, Microelectronic Circuits, 4ª edição, Oxford
- Boylestad, Robert l, Introductory Circuit Analysis, 8ª edição, Boylestad
- Dorf Richard C., Svoboda James A., Introduction Electric Circuits, 5ª edição, Wiley
- Chapman, Stephen J. – Java for Engineers and Scientists, 2nd Edition, Pearson – Prentice Hall
A applet "Circuitos RC/RLC e Filtros" foi criada por adaptação da aplicação Java, desenvolvida por Paula Nascimento no âmbito da disciplina de Projecto (3º ano do Bacharelato).